KEY ASPECTS AND HUBBLE'S LAW
STAR DISTANCE VALIDATION
THE 4-SPHERE METRIC TENSOR
ON EINSTEIN'S CONSTANT Λ
OTHER ASPECTS OF 4-SPHERE
THIS SPECULATION AND ARTIFICIAL INTELLIGENCE
EPISTEMOLOGICAL CONSIDERATIONS
The 4-Sphere model for an Alternative Metric in Cosmology
Proposing a different calculation for the Galactic Recession, we intend to show the opportunity to modify the Standard Cosmological Model ΛCDM choosing a new metric, other than FLRW.
|
License: Creative Commons Attribution-ShareAlike 4.0 International Public License
The 4-Sphere Metric Tensor
In a small portion of 4d-hypersphere's surface, where its spacetime can blend with that of our Universe, for the line element to be considered in the Einstein-Hilbert action, the following must hold: ds2 = gμνdxμdxν with xμ = x, y, z, t if we want Galilean coordinates.
Named ξ the angle at the center between two points, P1 and P2 on the surface, you can refer to the expanding arc of great circle rξ to simplify the reasoning on geodesics. It is therefore a question of describing a motion along a line in which the constraint reactions, induced by the line itself, must not appear in any Action Principle.
Thus, continuing with the idea that from the denial of Absolute Space, Relativity is deduced, let us start from a solution in the form: ds2 = −hrξ(drξ)2+htc2dt2
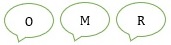 |
|
| and consider the differential of the product rξ: | d(rξ) = ctdξ + cξdt. |
- O is the overall motion, in part constrained by r = ct
- M is free motion along the expanding arc
- R is motion due to Galactic Recession
Then, for the recession it holds vr = cξ, while if we refer to Einstein's field equation, we can limit it to a small portion of the surface of the hypersphere, where we neglect the recession.
Here, the remaining expression for our interval ds2 = −hrξ (ctdξ)2+htc2dt2 reflects the expansion of the Universe. This is not a negligible phenomenon, and if we can only measure it through the observation of stars, it is because the objects around us are bound by gravitational forces that resist their mutual separation. Our nearby spatial references remain constant because they are determined by the cohesion of matter or by celestial bodies in stable orbits, gravitationally bound around a center of mass that is in constant recession. This allows us to assume r = ct = const. By arbitrarily setting ht = 1, the conditions dictated by the equivalence principle are satisfied by imposing that, at position O, for hrξct, there is a transition to Proper Coordinates, assuming a constant value ro with zero as its first derivatives. In this way, we obtain Special Relativity in Galilean coordinates x = roξ and t. Gravity would then be applied accordingly.
EXPLORING EXPANSION AND GRAVITY IN SIMPLE TERMS
In the case of uniform circular motion due to gravity, a peculiar situation arises in 4-Sphere: recession occurs at a constant velocity and in the absence of forces. If the recession occurs without work and given that in uniform circular motion the centripetal force also does not perform work, we must conclude that kinetic energy is conserved by adding the two perpendicular velocities vr and vt. Furthermore, in absence of new forces the quantity L = m vr+t r which represents the angular momentum is affected by the recession and the radius is smaller.
Consequently, to maintain the conservation of kinetic energy, the tangential velocity must increase, also leading to an increase in centripetal force.
And if the recession velocity were too high, the orbit could could not be compatible with the observational data.
But this unusual reasoning applies to recently formed orbits.
In 4-Sphere, the Last Scattering occurred without expansion, implying that the universe was static. After this, expansion began to increase progressively, only stabilizing in more recent cosmic history.
This interpretation suggests that during the early phases, when the universe was still dominated by plasma and radiation, nuclei of gas clouds (the precursors to galaxies) formed their orbital structures. These initial orbits, which were gravitationally bound, became stable before the expansion accelerated significantly. As a result, ancient structures like the Local Group, formed early in the universe's history, would have developed in a regime where the expansion did not disrupt their orbits.
Once these stable orbits were established, the subsequent expansion of the universe, although accelerating, could not affect these already-formed orbits. This addresses the issue of why galactic orbits, especially in older systems like the Local Group, remain stable despite the ongoing cosmic expansion. The acceleration of expansion, which became prominent only in the latter half of the universe’s history, would not retroactively influence these orbits.
By postulating that orbital structures formed before significant expansion, this model offers a solution to the question of why recession effects do not destabilize ancient galaxy groups.
TO SUM UP
To sum up, what we measure in our vicinity is a space that does not expand, where the true geometry has been altered. So we can conclude that, where gravity manifests, the Cartesian variable x can be merged with our arc ξ, so that Δx = ctΔξ thereby making the line element governed by a tensor. Cosmic expansion should be considered in the context of inter-group dynamics, between gravitationally bound systems like galaxy groups and clusters. However, within these systems (intra-group), the gravitational forces dominate, preventing the expansion from affecting the internal structure.In the inter-group context, the geodesic of light reduces to 0 = −(ctdξ)2 + c2(dt)2 (which gives v = c) and the redshift of a faraway star comes mainly from the recession vr = cξ. In the intra-group context, where regardless of the size of a celestial system none of its bodies are receding from each other, the redshift of a nearby star should be interpreted as its orbital velocity (or a peculiar velocity) and its distance should be calculated from its distance modulus μ. Finally, it is important to underline that, with regard to gravity and therefore in the intra-group context, we can apply Einstein’s field equations in their original form (with Λ = 0) [**].
For model use, the calculations applied weak field equations to the CMB, which expands in equilibrium, meaning that its density changes in the presence of forces that maintain balance. This approach assumes that gravity remains consistent with the isoentropic expansion. Thus, despite the long-term cosmic evolution, the model suggests that the gravitational effects align with the expanding, thermodynamic properties of the CMB, ensuring that the overall energy and forces in the universe remain in a state of equilibrium.
The line element proposed by the model includes a recession term, cξdt, which applies exclusively to stars (matter), while the second postulate of relativity (regarding light) is guaranteed by the assumed geometry. Thus, we accept superluminal speeds between physical entities, but only under the condition that these objects cannot be physically observed. We also accept relativity in all the laws governing our physics, including the 2 laws of conservation of mass and momentum and the relationship between mass and energy, because the model ensures that wherever relativity is manifested, the effect of recession term cξdt, which is completely absent in the case of light, can still be neglected in the case of matter. Recession is used only to calculate the effect on the light arriving from the star.
ABOUT ENERGY AND ENTROPY
To conclude this brief overview, I will outline the considerations regarding the energy and entropy of the Universe as a whole, based on this model that considers only the CMB, where its redshift is exclusively gravitational. In this model, the Universe is homogeneous (and uniform) at every point, meaning that physical properties such as energy and gravity are evenly distributed throughout.
Space is described as a four-dimensional spatial hyper-bubble that is continuously expanding, and where the CMB acts as a cohesive force, similar to the surface tension γ of a bubble:
‒ Energy: The CMB cannot be considered to be undergoing free expansion, nor can it be seen as expanding against external pressure forces. That said and given the premises, according to the principle of mass-energy conservation, energy of such a system changes when something happens on its surface. In other words, what happens at the system's boundary affects its total energy. However, even though the universe has a finite volume, it does not have edges or boundaries. How could we ever explain a change in energy? But let us look at the whole from a four-dimensional perspective! We have negated the concept of absolute space, and there is no external space outside the bubble.
In our analogy γAsurf = Esurf = EUniv: a change in energy EUniv then corresponds to a change in our surface tension analogue and/or in the three-dimensional surface area of the hypersphere. That is, the decrease in energy due to the increase in the wavelength of the CMB is due to the change in the equilibrium conditions of the expanding bubble.
The energy EUniv we measure is not the total energy. Indeed, it lacks the potential energy associated with the transformation process: a hypothetical potential in which is being stored the work done during the expansion [***].
If we add this component, we obtain an energy Etot that remains constant in our isolated system.
‒ Entropy: The expansion is adiabatic and occurs without friction, it occurs uniformly due to the absence of boundaries, just as the reverse process would. This is not comparable to the expansion of a gas in a piston which is irreversible at finite rate. It is governed solely by gravitational forces, which are conservative. Therefore, we must conclude that entropy is constant, even though the expansion does not occur at an infinitesimally slow rate. The conservation of entropy is fundamental not only to maintain the blackbody spectrum of the CMB but also to ensure the correct evolution of temperature and thus the energy of cosmic radiation over time. [****]
[*] – For a discussion on ancient galaxies, now in orbit around each other, but which may have always been, see chapter 5.5 in 4-SPHERE FEATURE AND SPECULATION.
[**] – See chapters 3.2 and 3.3 in 4-SPHERE FEATURE AND SPECULATION.
[***] – Let’s imagine a two-dimensional being living on the surface of a soap bubble. They would only be able to measure the surface tension of the bubble (their universe), without having access to what happens inside or outside of it. If they noticed that the surface energy was not constant over time, they might hypothesize the existence of a potential energy associated with the bubble to explain the observed behavior. However, this hypothesis would lead them to realize that their understanding of reality is incomplete.
[****] – The conjecture about the 4d bubble and the evolution of energy does not seem inconsistent. We can consider that the energy we measure, which is correlated to blackbody radiation, is a projection or a partial aspect of the total energy of the bubble in 4 dimensions. It's possible that the "real" energy includes components associated with dimensions that we do not directly perceive, but which influence the evolution of energy in the observable three-dimensional space. The apparent coincidence between the measured energy and that of blackbody radiation could be a consequence of a deeper principle, where the visible energy is only a portion of the actual energy, which includes contributions from the geometry of the 4D bubble. Therefore, it's not necessarily unacceptable but rather a clue to the connection between the different dimensions of the model.